Which Dice Did I Roll? (Age 7)

The Activities

1. Topic: Numbers: Book: The Number Devil by H. Enzensberger, Chapter 2.
2. Topics: Probability, Graphs: We revisited the activity from last week where we made two big charts, one for the sum of two six-sided dice, the other for a twelve-sided die.  This time, I wrote a computer program to simulate dice rolling, and ran it until the winning number came up 50 times.  I ran it twice each for 1d12, 2d6, and 3d4 (left to right below), and then copied each result into a chart.  Then, I showed the kids each chart and asked them how they thought I had made each of the charts.  We had only done 1d12 and 2d6 before, so including 3d4 was kind of cheating.
   
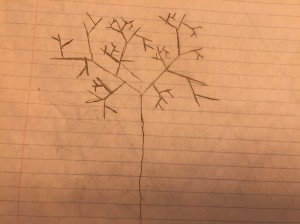
3. Topic: Spatial Reasoning: We continued the activity from last week where one kid made a shape using pattern blocks and then described it to the other kids.  This time I varied whether the kids worked individual, in one big group, or 2 small groups to follow the instructions.
   

   Original shape

   Copied shape

How Did It Go?

We had all five kids this week.

The Number Devil

We read most of the 2nd chapter, which talked about zero and how Roman numerals are unwieldy because they don’t have place values. We stopped and talked at a number of places, the kids were pretty involved.

Probability Charts

At first the kids didn’t want to volunteer many opinions. I had them vote on each one, for a while only one or two kids voted each time. After a while, they had grouped into two piles: (1d12, 1d12, 3d4) and (2d6, 2d6, 3d4). They decided 3d4 didn’t fit, and moved it to the other pile. So they got everything as right as possible. Then I told them that I had actually rolled 3d4 for 2 of them, and pointed out how 2 was missing on those charts and how 3 and 12 were so low. They thought it was cheating :).

Describing Shapes

We did 3 different patterns this time, the kids are getting increasingly ambitious in their patterns. The pictures above show one of the results. The top part was described as a flower; you can see that the petals are pointed in the wrong orientation. Also, the relationship between the three trapezoids wasn’t described. The final pattern was quite a bit more complicated, and I needed to help or they would have been way off (due to under specification of directions). They do well when the shapes are totally symmetric, because they can guess what it should look like.

Wizard of Oz Logic (Age 5)

The Activities

1. Topic: Logic: Book: The Case of the Missing Zebra Stripes by Time-Life Books. This time we did the chapter about the missing stripes.
2. Topic: Logic. Follow clues to put Wizard of Oz dolls in the correct order.
   

   The dolls in order.

   Puzzle #1: The wicked witches were first and last. The wicked witch of the east was next to Glinda. The hats of the same color were together. Dorothy held the Scarecrow’s hand. The wizard finished just before Glinda. (The picture is the answer to this one).

   Puzzle #2: The wicked witches are next to Dorothy. The scarecros is next to Glinda. The East finished after Dorothy. The boys were together. Glinda was first. The Wizard was next to a wicked witch.

   Puzzle #3: (Uses the lion and the tin man figures too). A boy won. Dorothy was next to Glinda. Pointy hats were together. Dorothy was third to last. The East pulled Glinda’s hair and finished before her. The first person was silver. The scarecrow finished before the East.

3. Topic: Sorting. Put the numbers 1-100 in order on the number board. This time, we did the side that does not show all the numbers.  I put in some numbers before they started to make it easier.
   

   The starting board.

4. Topic: Attributes. Build a chain using attribute blocks, so that each pair of adjacent shapes has only one difference.  For example, a big, fat, red, circle could go next to a big, fat, blue, circle.
   

   An attribute chain around the table.

   How did it go?

We had all five kids this week. They worked well together, but the activities were a little harder than usual, so some kids got distracted at various points.

The Zebra Stripes

The kids were all excited to get to the chapter that the book was named after. In this chapter, an investigator tries to figure out why some zebras are missing their stripes every day at 6pm. It turns out that those are not zebras, but white horses who jumped into the zebra’s pen to eat the zebra dinner.

One kid immediately noticed the white horses in the neighboring pen (on the first page of the chapter).  She even suggested that maybe the white horses were jumping in to the pen. Furthermore, she said we could count the zebras to check if that was happening.

Wizard of Oz Logic

First I showed the dolls to the kids.  Two of them were unfamiliar with the Wizard of Oz characters but quickly learned the characters’ names.  There was a bit of gr.abbiness during this activity, where everyone wanted to touch the dolls at once, but overall it went well.

Sorting

This was definitely trickier than the previous activity.  Two of the kids needed significant help to figure out where their numbers fit.  The other 3 could do it independently, but two of them made some mistakes (like thinking 68 was 86).

Attribute Chains

First we reviewed the attribute shapes and said what was the same or different about pairs of shapes.  Then I asked each kid to pick their favorite shape.  Then pick another shape that only has one difference.  With a bit of help, everyone found one.  Next I asked them to add to their chain. This took a bit of explaining to understand that you only look at the shapes right next to the new shape to count the differences, but eventually most kids understood.

After 10 minutes or so, we had 3 kids who had significant attributes chains of their own, and they started to overlap with each other.  At that point, the kids wanted to connect all their chains together.  So we all worked together to finish a large loop of the whole table. The kids were so excited that they brought in their parents to see what they had done.

Don’t Forget to Count the Feathers! (Age 5)

The Activities

1. Topics: Graphs, Measurement: Book: The Case of the Missing Zebra Stripes, Chapter 2.
2. Topic: Measurement: I gave each kid some twine and a pair of scissors.  Then I showed them some household objects (varying in size from ~3 inches to ~16 inches), and they had to cut pieces of twine of the right length without measuring, just by looking.
3. Topics: Addition, Games: We played the dice game again, where you roll a twelve-sided die and 5 six-sided dice (some of them 1-3 instead of 1-6) and try to make the number on twelve-sided die using addition and subtraction.
4. Topics: Geometry, Optimization: We had a bunch of “fences” (rectangular blocks) and small wooden animals.  The rules were you could make either rectangular or triangular pastures out of the fences; a 1×1 square could hold two animals, while an equilateral triangle of side 1 could hold one animal.  You could also omit fences between neighboring pastures (so you could make a parallelogram-shaped pasture, for example, which could hold two animals).  Also, you can’t mix animals within the same pasture.  Starting with 1 sheep, I asked what the minimum number of fences it takes to hold that number of animals is.  Then I added another sheep, asked how many fences, etc., until 12 sheep.  Then, I gave them 2 sheep, 2 horses, 2 donkeys, and 1 pig, and asked what the fewest number of fences was.

How Did It Go?

We had 4 kids this week.

Missing Zebra Stripes

This chapter was about making graphs to measure the heights of giraffes. There was also a part where you were supposed to say which was the longest lizard, or the longest bird. The lizards were curly, so you had to be careful; and I actually missed the fact that one of the birds had crazy tendril-like tail feathers, so we got the wrong answer (this came to light the following week when Corey read chapter 3).

Measuring with Twine

The first object (chapstick), the kids all did pretty well. But for the rest of the objects, most of the kids were way too high — often about 50% too long. One of the kids was WAY closer most of the time, and had the closest to the right answer every single time. It also happened that I had to go answer the door during this activity, and almost left behind the object they were supposed to be cutting twine for, but then I noticed that the kid who was doing the best started to reach for it to cheat. So they really wanted to win :).

Dice Game

There’s a very clear ordering of the kids for this activity, ranging from instantly getting it every time to having trouble adding up two dice even when given lots of time. And it’s not the same ordering as, say, the twine activity.

Building Fences

When I did this with the older kids’ circle, I didn’t introduce triangular areas, but it was a very nice addition and I’ll definitely keep it going forward. The solution to the final problem ended up involving triangles, and one of the kids came up with it without any help (in fact, it was better than the solution I had come up with). There was a lot of interesting experimentation with different arrangements of the fences. It seemed like they were starting to realize that square pens are more efficient than long skinny ones; but I don’t think they fully got the idea yet.

Cinderella’s Castle Vs. Elsa’s (Age 7)

The Activities

1. Topic: Graphs. Book: Graphs by Bader.A kid does his math homework at a family reunion by graphing various things. The kids all loved the surprise ending.
2. Topic: Probability, Graphs. The kids worked together to make two giant-sized probability graph.  Two kids filled in one graph by rolling two 6-sided dice and adding them together.  The other three kids rolled one 12-sided die to fill in theirs.
   

   One 12-sided die

   Two 6-sided dice.

3. Topic: Spatial Reasoning. The kids took turns building a secret shape out of pattern blocks.  The kid would then describe the shape to the other kids, who would try to build the same shape (without seeing the secret shape).

How did it go?

We had all 5 kids this circle.  It was a pretty easy circle, and everyone had a good time.

Big Probability Race

I broke the kids into two groups, to each work on one of the big graphs.  The graphs each covered and entire sheet of poster board.  Each kid had their own dice, and would roll, fill in a square, then roll again.

Kids at work.

After the a number won the race by reaching the top, I asked the kids if they saw any differences between the charts.  They said that the two  6-sided dice could never get a one.  But other than that, they felt that both graphs looked like castle.  The two dice one looked like “Cinderella’s Castle”, while the 12-sided one looked like Elsa’s castle because it was more jaggedy and had more towers.

I had expected the charts to look a little more different, but I think the kids rolling the 12-sided die were cheating a little.  They got a few extra 7’s at the start, and then really wanted to get more 7s, so they tended to skip some rolls that were not seven.

Shape Description

Four of the kids were excited to build and describe their own shape.  One kid chose not to do that, but he happily built the shapes the others described.

The describers learned a lot about what makes a good clue.  For example, one girl started by saying hers “looks kind of like a flower pot with three flowers”.  The other kids all groaned and complained because they had no idea what that meant.  With some help, eventually the describer finished, and the kids had similar answers:

Two answers to the “Pot of Flowers”

I wrote down some of the clues given by a later describer:

“Get 4 trapezoids, 6 triangles, 2 diamonds, 1 hexagon. The two trapezoids make a hexagon with the line going down. The two diamonds go on top of the trapezoid hexagon, pointing out. The hexagon goes on top of the diamonds, making a head shape.”

Secret Numbers and Secret Shapes (Age 5)

The Activities

1. Topic: Attributes, Estimation: Book: The Case of the Missing Zebra Stripes by Time-Life Books. This book has about 10 chapters all about different zoo-themed math activities. We did the first two chapters today.
2. Topic: Number Line: I have a number board that shows the numbers 1 – 100. I covered up numbers on the board and asked the kids which number was missing. Then I covered up 3 or 4 numbers in a row, and asked the kids.
3. Topic: Number Line, Number Guessing: Each kid picked a secret number between 1 and 100. The other kids took turns guessing the number. The secret kid would say whether their number was higher or lower than the number the kids had guessed.
4. Topic: Spatial Reasoning. One kid used pattern blocks to make a shape, out of sight of the other kids. Then the kid described the block arrangement, and the other kids tried to match.
   

   One kid’s shape.

How did it go?

All 5 kids attended today. We had a picnic for all the families after circle, so some of the kids were a little wild during circle. But overall it was a good circle.

Zoo Math

The first task was to estimate how many flamingos there are in a picture.  The kids initially guessed between a couple hundred and ‘ten hundred and twenty’.  I had one girl put her hand on the page, and counted that 10 flamingos fit under her hand. Then we found that it takes 15 of her hands to cover the page.  That means there could be 150 flamingos.  I then asked the kids for their final guess, and despite the estimation we had done, several kids still guess a couple thousand. The answer was 130.

The next chapter was a mystery about a new animal joining the zoo.  We got clues like: “The animal shares a trait with snakes, ostriches, and robins”.  The kids needed help to know that those animals all lay eggs. They were able to figure out the next two clues, that the animal was furry and had webbed feet.  None of them knew what animal that must be, but were able to pick out the platypus when looking a set of possible animals.

The chapter was followed by several “Odd One Out” puzzles, some of which were easy for the kids and some harder.  The kids were happy to all give their own theories. For example for the numbers “10, 11, 20, 30” one girl felt the 10 didn’t belong because it was smallest, which other kids thought 11 didn’t belong because it didn’t end in a 0.  One girl was especially good at articulating why something didn’t belong “I think the elephant doesn’t belong because the others are all birds”.

Number Lines

All the kids were pretty good at figuring out the missing number when just one number was covered, although a couple kids still got 68 and 86 confused.

Covering three numbers in a row was much harder.  A few kids would answer the first missing number, even if I was pointing at the second or third covered box.

After we did a few round of this, the kids all wanted to cover the board with the number tiles in order.  I handed out three numbered tiles at a time to the kids, who searched for the proper place to put them. Most of the kids were quick at this, though one boy still did exhaustive search to find where to put ’21’. He didn’t have a sense of whether 21 is a big or small number.  The kids were all excited to see who would be lucky enough to get the ‘100’ tile, but didn’t cry when someone else got it.

Number Guessing

Each kid got a chance to think of a number between 1 and 100. Then the other kids would try to guess it, and the secret kid would say whether their number was higher or lower than the guess.

The kids with the secret number were all pretty good at knowing whether to say higher or lower.  Only one kid got confused, and he seemed to understand after I took him aside and showed him where his secret number was on the board.

The kids loved to pick high numbers. 89, 90, 99, and 100 all got chosen.  The guessing kids were not good at binary searching for the numbers.  I helped them by pointing out that the number must be less than X, but they would still sometimes guess things higher than X.

Shape Description

Two weeks ago David had described shape arrangements, and the kids were very good at recreating the shapes.  This time the kids took turns making a secret arrangement, and describing it to the other friends.  They were actually all pretty good at describing their shapes, although sometime they weren’t precise enough so the friends would have different variations.

Fractal Hearts (Age 7)

The Activities

1. Topics: Geometry, Fractals: Book: Mysterious Patterns: Finding Fractals in Nature by S. Campbell.
2. Topics: Geometry, Fractals: I showed them how to make some standard fractals (tree, snowflake, Sierpinski triangle), and we spent some time drawing each of them.  Some of the kids also designed their own fractals.
3. Topics: Arithmetic, Order of Operations: We revisited the fives activity, where we tried to make as many numbers as possible using only fives and standard arithmetic operations.  Here’s the progress so far:
   

How Did It Go?

Mysterious Patterns

The kids were pretty interested in this book, and it led well into…

Drawing Fractals

We spent quite a bit of time on this; the kids would have happily done this the whole circle. Some of the invented fractals were pretty nice.

Fives

Some progress was made, but the kids aren’t as inventive as I might have expected. They’re especially hesitant to use subtraction, interestingly.