A Bag Full of Dice (Age 9)

The Activities

1. Topics: Geometry, Three Dimensional Shapes: Book:  Sir Cumference and the Sword in the Cone by C. Neuschwander.
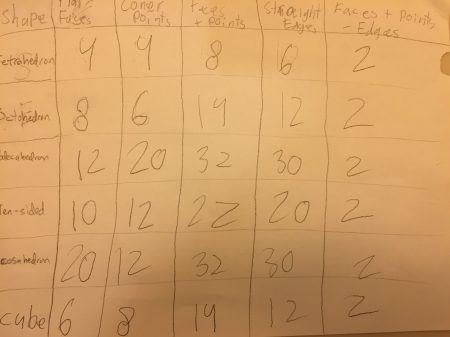
2. Topics: Geometry, Three Dimensional Shapes:  A while ago we bought 5 full sets of “D&D dice” (4, 6, 8, 10, 12, and 20 sided).  We counted the edges, faces, and vertices for each of these and made a chart like in Sir Cumference, showing that “Faces + Vertices – Edges = 2”.  I also pointed out the dual relationship between 6 & 8 and 12 & 20 sided polyhedra (i.e., 6-sided has 6 faces, 8 vertices, and 12 edges; 8-sided has 8 faces, 6 vertices, and 12 edges; you can switch between the two by putting a vertex in the middle of each face and connecting adjacent vertices).
3. Topic: Numbers: We did What’s the Secret Code? from youcubed.org.  There are some clues about what the secret number is like “The digit in the hundreds place is ¾ the digit in the thousands place.”  There is more than one answer which is cool.
4. Topics: Origami, Geometry: We did Paper Folding from youcubed.org.  There are a number of folding challenges like “Construct a square with exactly ¼ the area of the original square. Convince yourself that it is a square and has ¼ of the area.”

How Did It Go?

We had four kids this week.  As usual some kids followed along better than others, but most people were engaged for both the dice activity and the paper folding.

Sir Cumference and the Sword in the Cone

The kids liked the book, they laughed at quite a few of the math puns.

Euler’s Polyhedron Formula

The kids definitely enjoyed making the chart.  They did a pretty good job staying on task (it was easy to get distracted and start rolling the dice).  Counting the edges on some of the dice was fairly tricky but was much easier with good grouping strategies.

What’s the Secret Code?

The kids did well on this except that they had trouble with the decimals.  They did find one of the decimal answers, because they knew that .5 = 1/2, but I believe there were other possible decimal answers as well.

Paper Folding

The kids solved all the tasks except the last one, which was making a non-diagonal 1/2 area square.  I figured out a pretty complicated way to do it (by transferring the side length of the diagonal answer onto a horizontal edge), they copied what I did but it was pretty tricky (see picture above).

Odds & Ends (Age 7)

The Activities

1. Topic: Probability: Book: A Very Improbable Story by E. Einhorn.
2. Topic: Probability:  First, I secretly put 2 red and 8 blue stones into a small drawstring bag.  Each kid took turns pulling one stone out, looking at it, and then putting it back.  The question was, are there more reds or blues?  I repeated it with 4 red / 6 blue, and also 5 red / 5 blue.  Finally, I made two bags, one with 10 red / 10 blue, and the other with 11 red / 9 blue, divided the kids into two teams, and asked them to figure out which bag had more reds.  I gave the kids paper and pencil and they decided to make charts to keep track of the results.
   

   10 red / 10 blue

   

   11 red / 9 blue
3. Topics: Numbers, Sorting:  I had about 20 different numbers on squares of paper, 0, 1, 3, 4, 6, 8, 12, 13, 100, 105, 1001, 1052, 1053, 1000000, -5, and -100.  First, I handed each kid one number and asked them to sort themselves.  We did this several times, starting simple and then using some of the trickier numbers.  Then, instead of handing them the numbers, I taped a number to each kids’ back, and without telling each other what the numbers were, they needed to sort themselves.  We did this a few times as well.
4. Topics: Tangrams, Geometry:  I gave each kid six different tangram puzzles.  For the kids who finished earlier, I had them work on the letter “A” from Tangrams: 330 Puzzles.

How Did It Go?

We had four kids this week.  It was a good circle, a few of the kids got a little antsy when we were discussing the results of the bag counting, but otherwise they were all engaged the whole time.

A Very Improbable Story

The kids liked the cat on the head :).

Probability Bag

The kids immediately grasped the idea of looking for whichever color came out more often.  Not surprisingly, they were overconfident — once, after only 3 draws one kid concluded red was the winner and dumped out the bag, only to find out that there were 5 of each.

For the team activity, one of the teams delegated one person to pull the stones and the other to record, while the other was taking turns drawing out stones.  The former strategy was about 2x faster, so I suggested the other team use it as well.  It was very interesting to see the two charts (pictured above).  One was a standard tally chart, except with 6 instead of 5 in each group.  For the other, the kid started by writing a bunch of numbers, and then checking them off as stones were pulled out of the bag.  The results came out pretty nicely — exactly 50% for the 10/10 bag, and 55.6% for the 11/9 bag (expected 55%).  However, the kids were a bit confused by the fact that team 1 had counts of 15 red and 15 blue vs. 30 red and 24 blue for team 2 — at one point, one kid concluded that team 2 had more reds AND blues.  In fact, the only way I got them to conclude that team 2 had more reds was to ask them to guess what was in each bag.  Their guess for team 1 was 10/10, while their guess for team 2 was “6 more reds than blues” (not coincidentally, they had drawn red out 6 times more than blue).  I asked them how many reds there would be if there were 6 more reds than blues, and 20 total — this was actually quite hard for them and I had to help them a lot (the initial guess, 16, didn’t work).  Of course, 13/7 doesn’t match their observed results.  So, there’s clearly a lot more them to learn for the fine shades of probability!

Number Sorting

This activity was pretty easy for them, even with the numbers taped to their backs.  They had a lot of fun, particularly when I gave them negative numbers or really big numbers.  They did a great job not telling each other — the closest they came was saying one kid’s number was really low (when it was -100).

Tangrams

This group has done these puzzles before, but that wasn’t an issue, they didn’t remember the solutions.  They were better than last time, but the puzzles still definitely weren’t trivial.  The bonus puzzle is much harder because it wasn’t to scale, but they made a good effort and made progress.