A Trick-or-Treat Circle (Age 8)

The Activities

1. Topics: Proofs, Time, Logic:  I asked the kids to determine whether or not every year has at least one Friday the 13th.
   
2. Topics: Geometry, Time:  I made a map of a neighborhood for trick-or-treating.  The red house is your house.  Each inch of road is one block, and trick-or-treating along one block takes ten minutes.  First, I asked them how long it would take to trick-or-treat on every block (this requires repeating a few blocks).  Next, I asked what the most number of different blocks you could visit if you had 3 hours.  Finally, I asked how many different blocks you could visit if you had to return to your house to drop off candy every 5 blocks (i.e., after 40 houses).  A bonus question I didn’t get to was, if you wanted to minimize the time to visit every block, and you didn’t have to start at your house, where should you start?
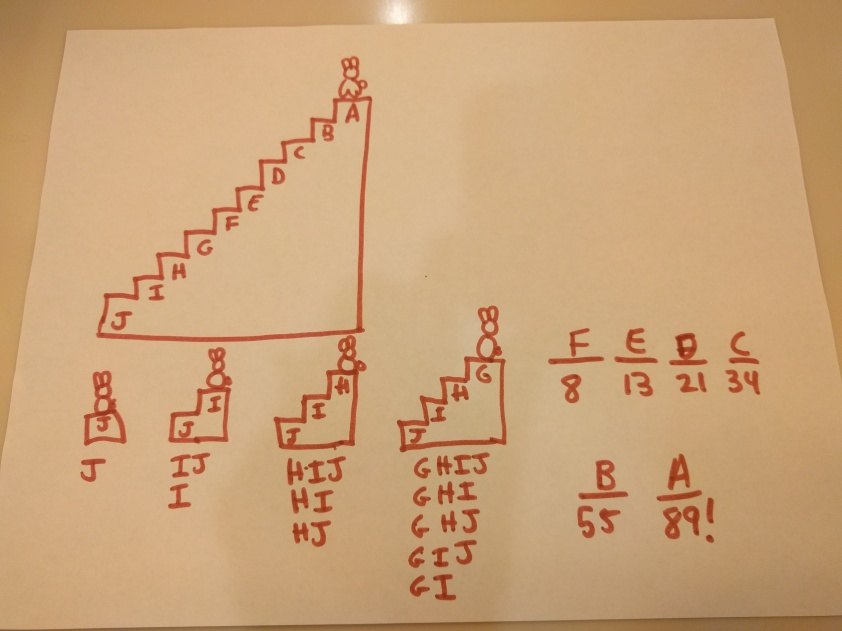
3. Topics: Combinations, Combinatorics, Logic:  I had a list of 10 possible trick-or-treaters:
   1. Evil Queen — Baddie, Girl
   2. Bride of Frankenstein — Baddie, Girl
   3. Vampire — Baddie, Boy
   4. Mummy — Baddie, Boy
   5. Princess — Goodie, Girl
   6. Fairy — Goodie, Girl
   7. Wizard — Goodie, Boy
   8. King — Goodie, Boy
   9. Alien — Neither, Neither
   10. Slime — Neither, Neither

   First, I asked how many ways there were to pick three trick-or-treaters.  Then I asked how many ways to pick three trick-or-treaters, with the requirement that there’s at least one Baddie, one Goodie, one Boy, and one Girl.  Note: Picking groups is much harder than picking ordered line-ups (where Evil Queen, Princess is different from Princess, Evil Queen).  If I were doing this again I would stick with ordered line-ups, it’s hard enough already.

How Did It Go?

We had all five kids this week.  This was a pretty hard circle; 2 of the kids were engaged through-out, with one saying how they liked the hard problems; the other 3 were distracted a lot of the time.

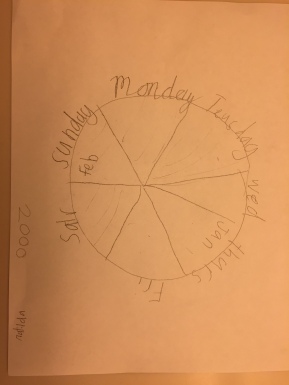
Friday the 13th

This is a pretty tricky problem, it’s not immediately obvious how to do it even for adults.  The kids made some good progress and had some interesting ideas.  First, one kid figured out that for there to be a Friday the 13th, the 1st had to be a Sunday.  Another kid wrote down the years starting with 2000 (she wanted to check “all the years”).  I used my phone to look up the calendars for each year, and we checked which months had a Friday the 13th each year.  One kid was really excited to try to find a year with no Friday the 13th, because then they’d be done.  But there is indeed a Friday the 13th each year, so we didn’t find one :).  At this point, I gave them a hint, which is to draw a pie chart like in the picture above.  The idea is to go through an entire year starting with January, assume that the 13th in January is, say, a Sunday, and then figure out what day of the week the 13th is in each month.  If you do this, you’ll find that every single piece of the pie is filled, which is what you need to prove that there’s always a Friday the 13th.  Unfortunately, the kids were not good at doing the calendar arithmetic to figure out what day of the week Feb 13 is given the day of the week for Jan 13.  So, we didn’t get that far, and since we had already spent 25 minutes I moved on to the next activity.  Most of the time, two of the kids were working on the problem while the others were drawing, etc.

Trick-or-Treat Optimization

The kids liked the theme of optimizing trick-or-treating.  Unfortunately, I made an error in how I set up the problem.  My intention was that they should concentrate on how many blocks you’d have to walk, but I drew the houses big enough that they focused on visiting houses instead of walking along blocks.  The map I included above I redid afterwards to make it clearer that it’s about blocks, not houses.  The problem with houses is that if you have houses on the corners of streets, it makes the counting a lot messier.  And counting houses is a bit more intuitive, so that’s what they defaulted to.  The result of this was that about half the kids thought I meant that it took 10 minutes to visit three houses, when I actually meant it took 10 minutes to walk one block.  All the kids paid attention during this activity.

The kids figured out that you’d have to backtrack or at least revisit some blocks.  They were all pretty comfortable with figuring out how long it would take to visit all the blocks, but the idea of the best route wasn’t as compelling.  They did understand the idea of visiting as many as possible in 3 hours.  The final problem, about returning home each time, isn’t actually that interesting with the map I had, but they still had to think about it some to figure out how to do it.

Picking Trick-or-Treaters

This problem turned out to be harder than I expected.  I just forgot that they weren’t that comfortable with combinations yet.  Even if I had done the ordered line version, they still didn’t immediately remember how to do the multiplication to figure out the answer to the unconstrained version.  They did figure out this part, and we moved on to the constrained version.

I actually gave them a four person version that required 2 baddies instead of 1 — it turns out to be a lot harder than the three person version.  Also, the non-ordered version is a lot harder to think about.  With the three person version, it’s not so bad to reason along the lines of “Let’s pick the baddy first, and the goody second.  For each of the possible combinations (there’s only 4 distinct ones), we can figure out what the third person can be.”  The four-person version gets a lot more complicated, so I switched to the three-person version — we made some progress but didn’t solve it.

Again, two of the kids worked hard, while the other three were distracted.

Trick or Treat Math (Age 6)

The Activities

1. Topic: Counting. Book: How Many Donkeys? An Arabic Counting Tale, by MacDonald. In this simple book a man can’t figure out if he has 9 or 10 donkeys because he keeps forgetting to count the donkey he is riding. The kids caught on quickly and laughed whenever he got it wrong.
2. Topic: Maps, Spatial Reasoning, Logic: Fill in a map of a treat-or-treating neighborhood based on the following clues. Here is the clipart we used: halloweencharacters.
   1. Directly to the West of your house is the Witch’s house.
   2. The Zombie house is 2 houses West of the Witch’s house.
   3. Olaf’s house is across the street from the Zombie’s house.
   4. Elsa’s house is directly South of the Witch’s house.
   5. The pumpkin house is directly East of your house.
   6. The Spider house is on the very West end of the South side of the street.
   7. The Butterfly is scared of the Spider. The Butterfly’s house is on the same side of the street as the Spider’s, but as far away as possible.
   8. The Goblin is between the Zombie and the Witch.
   9. The skeleton is directly across the street from the Spider.
   10. Next to Elsa’s house is a Graveyard that takes up two houses.
   11. The Ladybug’s house is right next to the Butterfly’s.
   12. The Fairy can fly right across the street to the Ladybug’s house.
   13. The Wizard’s house is East of the Fairy’s.
   14. Anna’s house is next to Elsa’s house.
       

       The completed puzzle

       3. Topic: Estimation, Subtraction. Guess how much candy is in a container. Then put the same candy in a shallower container and guess again. Then count the candy and figure out whose guesses were the closest.

       

       The Candy

       4. Topic: Logic. Tape a Halloween character to each kid’s head. Then the kids ask each other yes/no questions to figure out who they are. The hardest part of the game is not telling your friends what is written on their heads.

       

       

       How did it go?

       I wore my witch costume during circle, and I organized it so the kids would get to ‘trick or treat’ after completing each activity from my bucket of small prizes and candy.

       Halloween Logic

       Each clue was pretty easy for kids, especially after they understood what phrases like “directly West” means. The hardest clue was: “The Spider house is on the very West end of the South side of the street.” Two of the kids figured it out on their own. The other two needed some help from their friends to understand the “south side of the street”.

Candy Estimation

The kids were very excited to see so much candy, especially when I told them that the person who guesses closest would get to trick or treat twice after the activity. Interestingly, the guesses did not get closer after I spread out the candy. Most second guesses were at least as wrong as the first guess. I guessed after the candy was spread out (and I got within 2 of the correct number).

After everyone wrote down their guesses I asked the kids to count the candy. They immediately began discussing counting strategies. They eventually decided to sort the candy by type and then count each type. However, they soon realized that some types had too many pieces to be easily counted, and they didn’t know how to add the results anyway. So they switched to counting each piece of candy as it was thrown back into the tub. Two kids both wanted to throw in candy and everyone ended up missing a bunch of pieces when the two throwers could not coordinate. They came up with 67 pieces, but I counted it again and found 72 pieces.

Halloween Twenty Questions

The kids loved seeing costumes taped to their friends’ heads, especially when one boy got ‘Princess Leia’. I told them at the start that it is very important not to tell your friends what is written on their heads, and the kids did pretty well at this. However, some kids asked questions like “Am I a zombie?” because they saw “Zombie” on their friend’s head. The hardest to get turned out to be superman. The kid knew he was a strong hero who wears red and blue, and has an S, and has a cape, but couldn’t think of superman.  Everyone else figured theirs out eventually (with some hints from me about what questions to ask). Everyone really enjoyed this activity. At the end, we had five minutes left so one of the kids moms played and had to figure out she was a pumpkin. The kids loved hearing her questions and shouting out answers. “Can you eat me?” “Yes, but it’s yucky and too chewy!”

Impossible Flips (Age 6)

The Activities

1. Topic: Puzzles:  Book: Taro Gomi’s Playful Puzzles for Little Hands.  Still haven’t quite finished, this time it was mostly mazes.
2. Topics: Number Line, Number Recognition.  We revisited higher/lower number guessing again, mostly from 1-100.  As usual, the theme of the game was a bear who wants to steal our picnic food.  But the bear print-out was missing so kids took turns standing next to the wall and using their finger as the bear.  I did a few numbers, and then each kid took turns thinking of their own number.  At the end, we had a discussion about what makes a good or bad guess, and then I did one from 1-1000.
3. Topics: Combinatorics, Geometry:  Using wooden pattern blocks, find as many ways as possible to make a 2×2 diamond.
4.  Topic: Logic:  We did the Seven Flipped activity from youcubed.org.  Starting with 7 shapes face-down (we used Scrabble tiles), you could flip 3 tiles at a time.  The goal is to flip all the tiles face up.  After they solved that, I switched to 7 tiles, flip 4 at a time (which is impossible) and then 5 tiles flip 2 (also impossible), and we discussed why it might be impossible.

How Did It Go?

We had all five kids this week.

Number Guessing

There is a very wide range of abilities in this game.  By the end, three of the kids completely understood how the game worked, and during the discussion two of them worked together to figure out that they should guess half-way in between each time.  One of the other kids usually made proper guesses, but the final kid frequently made guesses outside of the current range (even when they were just reminded of what the current range was).  I also made a couple “illegal” guesses when I was playing, but was called out on it.  1-1000 is still pretty challenging even for the kids that get it.

Diamond Variants

The kids weren’t as in to this activity as I expected.  A couple of them went off task pretty quickly, building whatever they felt like.  One kid tried hard to use the skinny white diamonds, which doesn’t work.  Another kid was trying but kept building diamonds that were 3 units on the side.  One kid tried for a while to use squares, without success, but then eventually figured out a key insight for building different diamonds, which is that you can swap two adjacent triangles for a diamond, or vice-versa.  So that kid generated more than half of the variants we found.

Seven Flipped

The kids each had their own set of tiles.  There was lots of cheating, but it didn’t matter because I would just ask them to show me again.  At first the kids decided it wasn’t possible, but after a few minutes one of the kids figured it out.  Another kid watched them demonstrate, and then the two of them taught the other three.  Then I switched to 7/4.  There were lots and lots of claims of having done it, but it’s impossible :).  After a while, I asked them to try 5/2 instead.  A couple of the kids started to get the idea that it was impossible.  I myself made a bunch of moves on this problem with the kids watching, and we kept track of how many were face up.  With a hint the kids noticed is was only 0, 2, and 4.  I made a set of maybe 11 tiles with 6 flipped up, and then showed them all the possible moves (2 down -> 2 up, 2 up -> 2 down, and 1 up, 1 down -> 1 down, 1 up), and they saw that it could only be +2, -2, or 0.  One or two of the kids might have understood this proof that 5/2 is impossible.

Leo the Rabbit (Age 8)

The Activities

1. Topic: Logic. Book: Still More Stories to Solve by Shannon, Stories 11 – 14. The kids absolutely love this book of brain teaser stories, like what can you say to your two enemies to make them fight each other and leave you alone? Or how can a man get two wishes fulfilled when the genie only grants one wish? We spent about 25 minutes discussing the four stories we read. Most of them we could not solve on our own, but I would read the answer and give hints. Everyone understood the answers at the end.
2. Topic: Logic, Combinations. We got this problem from the awesome site YouCubed.org. Leo the Rabbit is at the top of a staircase of ten steps. Leo can h0p down either one or two steps at a time. How many different ways can Leo hop down the stairs?
3. Topic: Counting, Geometry. How many rhombuses are there in a heart made out of the YouCubed logo?

 

How did it go?

This was our first circle in a month, due to traveling. All five kids attended. This was a very high-energy circle, especially for my daughter who was having trouble staying on task. For each activity there were a couple kids complaining they were bored, but also at least a couple who stayed interested and learned something. I had a lot fun actually, because I intentionally didn’t solve the Leo the Rabbit problem ahead of time, and it was exciting to figure it out during circle.

Leo the Rabbit

First we started by drawing the rabbit at the top of a set of 10 stairs. We assigned a letter to each stair, and then each kid wrote a bunch of letter sequences representing the hops the rabbit makes. Kids came up with about 10 paths each before they started to want to find a faster way. My daughter suggested that you could first find all the paths that start with AB, and then all the paths that start AC.  I used this as a starting point. I asked the kids to consider just the last three steps in the staircase. If Leo is on step H, how many ways can he get to the bottom? Several kids were able to enumerate the 3 possibilities: HIJ, HI, or HJ.

Then I added step G. Now how many ways?  I pointed out that if the rabbit hops to step H, then his choices are now the same as the three ways we found for step H, namely: GHIJ, HI, GHJ. But Leo could skip step H, so we have to add in GIJ and GI as possibilities. Some kids understood this, but most did not. So I started even simpler.

What if there is only one step, step J? Then there is only one choice: J.

I ended up drawing a picture similiar to this:

At least one kid really seemed to understand that to get the ways for Step N, you add together the ways down from N-1 and N-2 (since Leo could hop down to either of those). All the kids soon saw that to fill in the next step, you should add the numbers from the two steps below, but many of them probably did not fully understand why. We were all impressed to get 89 ways, and were glad we didn’t try to enumerate them all.

Everyone started out quite engaged during this activity, but people started dropping off and getting distracted. In the end, 3 of the kids were still paying attention and 2 were quite ready for the activity to end.

YouCubed Heart

I intentionally made this activity much easier. YouCubed has a number of interesting questions about the picture, but I just asked how many rhombuses there were, and then let them color the picture for the last five minutes of circle.