The Bird and the Bikes (Age 9)

The Activities

1. Topic: Money. Book: The Story of Money by Maestro.  We continued where we left off last time, and got as far as early money in the Americas.  My favorite part was the discussion of why paper money caught on better in China than in Europe (the government was more stable in China).
2. Topics: Algebra, Arithmetic:  I wrote down the equation (5789 + 1286) x 549 = 3,884,175.  I used my phone to compute the right hand side.  Then I asked them a series of questions: What is the answer if you change 5789 to 5790 (the answer increases by 549)?  What if you change 549 to 550?  What if you change 549 to 1098?  Each time, using my phone, I checked that you got the same answer by evaluating directly vs. evaluating incrementally.
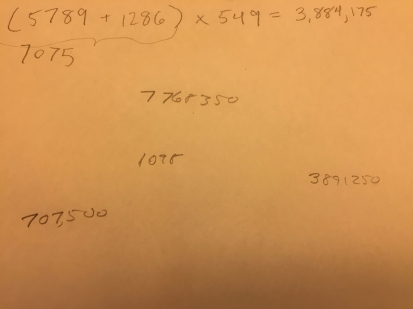
3. Topic: Probability: I attempted to teach the kids how to flip a coin properly, and then each kid (and me) spent 5-10 minutes flipping coins and writing down the sequence.  Then, I asked several questions: “Do you expect more heads or tails?  Is heads more likely after you’ve just gotten three tails in a row?  Is heads-tails more likely than heads-heads?”  For each one, we counted in our sequences to see whether the results matched the kids’ intuitions.
   
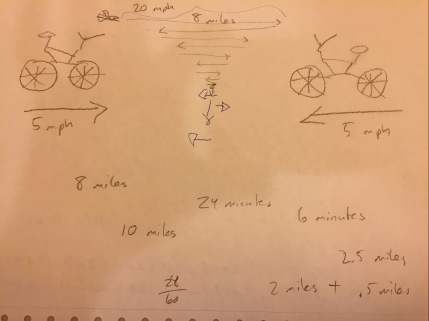
4. Topic: Logic: I drew a picture of two bicycles riding toward each other at 5 mph, starting 10 miles apart, and asked them how long before the bicycles met.  Then, I added a bird flying at 20 mph back and forth between the bicycles, turning around and going back whenever is met a bicycle, and asked how far the bird flew before the bikes met.

How Did It Go?

We had four kids this week.  It was a pretty good circle, some distractions as always but a lot of good thinking as well.

The Story of Money

This book has been going well, our daughter was able to explain the China vs. Europe paper money difference later that day when we were talking about circle.

Incremental Algebra

The kids did quite well on this activity, many of them were comfortable with parentheses and they didn’t have much problem getting the right answers.  By the end they were getting confident enough they thought the checking was a waste of time.

Coin Flip Sequences

When I started asking questions, I got some answers like “more heads after 3 tails in a row” — but I was surprised that after hearing each others’ answers they quickly converged to 50/50 no matter what.  So they seem to have a decent grasp on the idea of independence of coin flips.  Flipping was kind of hard for them, they really wanted to move their whole hands instead of just their thumbs.  For this reason the results were slightly suspect.  And of course this is a probability exercise so the results never come out perfect.  But by the end I felt pretty confident that some of the kids understood the idea of evaluating probabilities by counting occurrences from a sequence of trials (i.e., statistics).  The trickiest part was that if you have a sequence of, say, 5 heads in a row, and you’re counting outcomes after 3 heads in a row, you use this sequence 3 times (first 3, second 3, and final 3).

The Bird and the Bikes

One of the kids got the clever answer to the full question almost immediately.  Partly this was because I made it easier by asking the bikes only question first.  But still, I was impressed.  We also started computing the “brute force” way where we figured out how far the bird flew before meeting the first bike (8 miles).  The kids did okay at this too even though it’s a bit tricky.

Robots, Planes, and Pie (Age 8)

The Activities

1. Topics: Puzzles, Arithmetic: Book: Edgar Allan Poe’s Pie: Math Puzzlers in Classic Poems by J. Patrick Lewis.  We read 5 or 6 of the poems and they solved the math puzzle.  For some of the poems, I found the original version and read it to them first.
   

   
2. Topics: Logic, Hard Problems: You have available an unlimited number of airplanes.  Each airplane can hold 12 units of fuel, and the airplanes can refuel each other in midair.  Each unit of fuel lets an airplane go 1000 miles.  Airplanes can only land at the starting line — if they run out of fuel anywhere else they crash.  I asked the kids to try to get as far from the starting line as possible without having any planes crash.  I created a powerpoint with planes and distance track as a visual aid — the planes show the fuel units and the kids could fill in the units in pencil as they simulated their solution.
3. Topics: Counting, Factors: We did the Robot Stepper activity from youcubed.org.  I made a square grid of the numbers from 1-100 for the kids to fill in, and gave each kid a different starting number and number of steps.  After each kid had done several different charts, we looked at them as a group to see what kind of patterns we could find.
   

How Did It Go?

We had all five kids this week.

Edgar Allan Poe’s Pie

The kids liked the puzzles and did a pretty good job listening and trying to solve them.  However, they weren’t very interested in hearing the original poems, some of them said they were boring or “Why are we doing this?”  I was surprised because I thought they might like the change of pace.

Long-Range Airplanes

As is often the case on this kind of problem, a couple of the kids tried hard and the rest were distracted most of the time.  They all liked the planes — one kid was even grabbing other kids’ planes :(.  One of the kids made quite a bit of progress.  I gave the kids a way to get to 7 using 2 planes (they both move 4 spaces, one plane gives 2 fuel and returns home, other plane has enough to get to 7 and then back home); the one kid quickly figured out you can get to 8 using 2 planes, and kept improving until they got a plane to distance 12 and back (using 5 or 6 planes, can’t remember).  Framing the problem as “How far can you get?” rather than “Can you get to X?” was good, I think, because it took the pressure off.

Robot Stepper

Everyone was into making the charts.  One kid made a couple mistakes, decided to X out the mistakes, and then decided to go ahead and X out every skipped square.  All the kids noticed patterns as they were coloring, and often stopped actually counting and just used the pattern instead.  The best insight on this problem was one kid was able to explain why stepping by 9 created a backwards diagonal (going down adds 10, going to the left subtracts 1).  Unfortunately the kids weren’t super interested at the end when we laid out all the diagrams and analyzed them, but maybe it’s just because circle was almost over at that point.

A Trick-or-Treat Circle (Age 8)

The Activities

1. Topics: Proofs, Time, Logic:  I asked the kids to determine whether or not every year has at least one Friday the 13th.
   
2. Topics: Geometry, Time:  I made a map of a neighborhood for trick-or-treating.  The red house is your house.  Each inch of road is one block, and trick-or-treating along one block takes ten minutes.  First, I asked them how long it would take to trick-or-treat on every block (this requires repeating a few blocks).  Next, I asked what the most number of different blocks you could visit if you had 3 hours.  Finally, I asked how many different blocks you could visit if you had to return to your house to drop off candy every 5 blocks (i.e., after 40 houses).  A bonus question I didn’t get to was, if you wanted to minimize the time to visit every block, and you didn’t have to start at your house, where should you start?
3. Topics: Combinations, Combinatorics, Logic:  I had a list of 10 possible trick-or-treaters:
   1. Evil Queen — Baddie, Girl
   2. Bride of Frankenstein — Baddie, Girl
   3. Vampire — Baddie, Boy
   4. Mummy — Baddie, Boy
   5. Princess — Goodie, Girl
   6. Fairy — Goodie, Girl
   7. Wizard — Goodie, Boy
   8. King — Goodie, Boy
   9. Alien — Neither, Neither
   10. Slime — Neither, Neither

   First, I asked how many ways there were to pick three trick-or-treaters.  Then I asked how many ways to pick three trick-or-treaters, with the requirement that there’s at least one Baddie, one Goodie, one Boy, and one Girl.  Note: Picking groups is much harder than picking ordered line-ups (where Evil Queen, Princess is different from Princess, Evil Queen).  If I were doing this again I would stick with ordered line-ups, it’s hard enough already.

How Did It Go?

We had all five kids this week.  This was a pretty hard circle; 2 of the kids were engaged through-out, with one saying how they liked the hard problems; the other 3 were distracted a lot of the time.

Friday the 13th

This is a pretty tricky problem, it’s not immediately obvious how to do it even for adults.  The kids made some good progress and had some interesting ideas.  First, one kid figured out that for there to be a Friday the 13th, the 1st had to be a Sunday.  Another kid wrote down the years starting with 2000 (she wanted to check “all the years”).  I used my phone to look up the calendars for each year, and we checked which months had a Friday the 13th each year.  One kid was really excited to try to find a year with no Friday the 13th, because then they’d be done.  But there is indeed a Friday the 13th each year, so we didn’t find one :).  At this point, I gave them a hint, which is to draw a pie chart like in the picture above.  The idea is to go through an entire year starting with January, assume that the 13th in January is, say, a Sunday, and then figure out what day of the week the 13th is in each month.  If you do this, you’ll find that every single piece of the pie is filled, which is what you need to prove that there’s always a Friday the 13th.  Unfortunately, the kids were not good at doing the calendar arithmetic to figure out what day of the week Feb 13 is given the day of the week for Jan 13.  So, we didn’t get that far, and since we had already spent 25 minutes I moved on to the next activity.  Most of the time, two of the kids were working on the problem while the others were drawing, etc.

Trick-or-Treat Optimization

The kids liked the theme of optimizing trick-or-treating.  Unfortunately, I made an error in how I set up the problem.  My intention was that they should concentrate on how many blocks you’d have to walk, but I drew the houses big enough that they focused on visiting houses instead of walking along blocks.  The map I included above I redid afterwards to make it clearer that it’s about blocks, not houses.  The problem with houses is that if you have houses on the corners of streets, it makes the counting a lot messier.  And counting houses is a bit more intuitive, so that’s what they defaulted to.  The result of this was that about half the kids thought I meant that it took 10 minutes to visit three houses, when I actually meant it took 10 minutes to walk one block.  All the kids paid attention during this activity.

The kids figured out that you’d have to backtrack or at least revisit some blocks.  They were all pretty comfortable with figuring out how long it would take to visit all the blocks, but the idea of the best route wasn’t as compelling.  They did understand the idea of visiting as many as possible in 3 hours.  The final problem, about returning home each time, isn’t actually that interesting with the map I had, but they still had to think about it some to figure out how to do it.

Picking Trick-or-Treaters

This problem turned out to be harder than I expected.  I just forgot that they weren’t that comfortable with combinations yet.  Even if I had done the ordered line version, they still didn’t immediately remember how to do the multiplication to figure out the answer to the unconstrained version.  They did figure out this part, and we moved on to the constrained version.

I actually gave them a four person version that required 2 baddies instead of 1 — it turns out to be a lot harder than the three person version.  Also, the non-ordered version is a lot harder to think about.  With the three person version, it’s not so bad to reason along the lines of “Let’s pick the baddy first, and the goody second.  For each of the possible combinations (there’s only 4 distinct ones), we can figure out what the third person can be.”  The four-person version gets a lot more complicated, so I switched to the three-person version — we made some progress but didn’t solve it.

Again, two of the kids worked hard, while the other three were distracted.

Trick or Treat Math (Age 6)

The Activities

1. Topic: Counting. Book: How Many Donkeys? An Arabic Counting Tale, by MacDonald. In this simple book a man can’t figure out if he has 9 or 10 donkeys because he keeps forgetting to count the donkey he is riding. The kids caught on quickly and laughed whenever he got it wrong.
2. Topic: Maps, Spatial Reasoning, Logic: Fill in a map of a treat-or-treating neighborhood based on the following clues. Here is the clipart we used: halloweencharacters.
   1. Directly to the West of your house is the Witch’s house.
   2. The Zombie house is 2 houses West of the Witch’s house.
   3. Olaf’s house is across the street from the Zombie’s house.
   4. Elsa’s house is directly South of the Witch’s house.
   5. The pumpkin house is directly East of your house.
   6. The Spider house is on the very West end of the South side of the street.
   7. The Butterfly is scared of the Spider. The Butterfly’s house is on the same side of the street as the Spider’s, but as far away as possible.
   8. The Goblin is between the Zombie and the Witch.
   9. The skeleton is directly across the street from the Spider.
   10. Next to Elsa’s house is a Graveyard that takes up two houses.
   11. The Ladybug’s house is right next to the Butterfly’s.
   12. The Fairy can fly right across the street to the Ladybug’s house.
   13. The Wizard’s house is East of the Fairy’s.
   14. Anna’s house is next to Elsa’s house.
       

       The completed puzzle

       3. Topic: Estimation, Subtraction. Guess how much candy is in a container. Then put the same candy in a shallower container and guess again. Then count the candy and figure out whose guesses were the closest.

       

       The Candy

       4. Topic: Logic. Tape a Halloween character to each kid’s head. Then the kids ask each other yes/no questions to figure out who they are. The hardest part of the game is not telling your friends what is written on their heads.

       

       

       How did it go?

       I wore my witch costume during circle, and I organized it so the kids would get to ‘trick or treat’ after completing each activity from my bucket of small prizes and candy.

       Halloween Logic

       Each clue was pretty easy for kids, especially after they understood what phrases like “directly West” means. The hardest clue was: “The Spider house is on the very West end of the South side of the street.” Two of the kids figured it out on their own. The other two needed some help from their friends to understand the “south side of the street”.

Candy Estimation

The kids were very excited to see so much candy, especially when I told them that the person who guesses closest would get to trick or treat twice after the activity. Interestingly, the guesses did not get closer after I spread out the candy. Most second guesses were at least as wrong as the first guess. I guessed after the candy was spread out (and I got within 2 of the correct number).

After everyone wrote down their guesses I asked the kids to count the candy. They immediately began discussing counting strategies. They eventually decided to sort the candy by type and then count each type. However, they soon realized that some types had too many pieces to be easily counted, and they didn’t know how to add the results anyway. So they switched to counting each piece of candy as it was thrown back into the tub. Two kids both wanted to throw in candy and everyone ended up missing a bunch of pieces when the two throwers could not coordinate. They came up with 67 pieces, but I counted it again and found 72 pieces.

Halloween Twenty Questions

The kids loved seeing costumes taped to their friends’ heads, especially when one boy got ‘Princess Leia’. I told them at the start that it is very important not to tell your friends what is written on their heads, and the kids did pretty well at this. However, some kids asked questions like “Am I a zombie?” because they saw “Zombie” on their friend’s head. The hardest to get turned out to be superman. The kid knew he was a strong hero who wears red and blue, and has an S, and has a cape, but couldn’t think of superman.  Everyone else figured theirs out eventually (with some hints from me about what questions to ask). Everyone really enjoyed this activity. At the end, we had five minutes left so one of the kids moms played and had to figure out she was a pumpkin. The kids loved hearing her questions and shouting out answers. “Can you eat me?” “Yes, but it’s yucky and too chewy!”

Impossible Flips (Age 6)

The Activities

1. Topic: Puzzles:  Book: Taro Gomi’s Playful Puzzles for Little Hands.  Still haven’t quite finished, this time it was mostly mazes.
2. Topics: Number Line, Number Recognition.  We revisited higher/lower number guessing again, mostly from 1-100.  As usual, the theme of the game was a bear who wants to steal our picnic food.  But the bear print-out was missing so kids took turns standing next to the wall and using their finger as the bear.  I did a few numbers, and then each kid took turns thinking of their own number.  At the end, we had a discussion about what makes a good or bad guess, and then I did one from 1-1000.
3. Topics: Combinatorics, Geometry:  Using wooden pattern blocks, find as many ways as possible to make a 2×2 diamond.
4.  Topic: Logic:  We did the Seven Flipped activity from youcubed.org.  Starting with 7 shapes face-down (we used Scrabble tiles), you could flip 3 tiles at a time.  The goal is to flip all the tiles face up.  After they solved that, I switched to 7 tiles, flip 4 at a time (which is impossible) and then 5 tiles flip 2 (also impossible), and we discussed why it might be impossible.

How Did It Go?

We had all five kids this week.

Number Guessing

There is a very wide range of abilities in this game.  By the end, three of the kids completely understood how the game worked, and during the discussion two of them worked together to figure out that they should guess half-way in between each time.  One of the other kids usually made proper guesses, but the final kid frequently made guesses outside of the current range (even when they were just reminded of what the current range was).  I also made a couple “illegal” guesses when I was playing, but was called out on it.  1-1000 is still pretty challenging even for the kids that get it.

Diamond Variants

The kids weren’t as in to this activity as I expected.  A couple of them went off task pretty quickly, building whatever they felt like.  One kid tried hard to use the skinny white diamonds, which doesn’t work.  Another kid was trying but kept building diamonds that were 3 units on the side.  One kid tried for a while to use squares, without success, but then eventually figured out a key insight for building different diamonds, which is that you can swap two adjacent triangles for a diamond, or vice-versa.  So that kid generated more than half of the variants we found.

Seven Flipped

The kids each had their own set of tiles.  There was lots of cheating, but it didn’t matter because I would just ask them to show me again.  At first the kids decided it wasn’t possible, but after a few minutes one of the kids figured it out.  Another kid watched them demonstrate, and then the two of them taught the other three.  Then I switched to 7/4.  There were lots and lots of claims of having done it, but it’s impossible :).  After a while, I asked them to try 5/2 instead.  A couple of the kids started to get the idea that it was impossible.  I myself made a bunch of moves on this problem with the kids watching, and we kept track of how many were face up.  With a hint the kids noticed is was only 0, 2, and 4.  I made a set of maybe 11 tiles with 6 flipped up, and then showed them all the possible moves (2 down -> 2 up, 2 up -> 2 down, and 1 up, 1 down -> 1 down, 1 up), and they saw that it could only be +2, -2, or 0.  One or two of the kids might have understood this proof that 5/2 is impossible.

Leo the Rabbit (Age 8)

The Activities

1. Topic: Logic. Book: Still More Stories to Solve by Shannon, Stories 11 – 14. The kids absolutely love this book of brain teaser stories, like what can you say to your two enemies to make them fight each other and leave you alone? Or how can a man get two wishes fulfilled when the genie only grants one wish? We spent about 25 minutes discussing the four stories we read. Most of them we could not solve on our own, but I would read the answer and give hints. Everyone understood the answers at the end.
2. Topic: Logic, Combinations. We got this problem from the awesome site YouCubed.org. Leo the Rabbit is at the top of a staircase of ten steps. Leo can h0p down either one or two steps at a time. How many different ways can Leo hop down the stairs?
3. Topic: Counting, Geometry. How many rhombuses are there in a heart made out of the YouCubed logo?

 

How did it go?

This was our first circle in a month, due to traveling. All five kids attended. This was a very high-energy circle, especially for my daughter who was having trouble staying on task. For each activity there were a couple kids complaining they were bored, but also at least a couple who stayed interested and learned something. I had a lot fun actually, because I intentionally didn’t solve the Leo the Rabbit problem ahead of time, and it was exciting to figure it out during circle.

Leo the Rabbit

First we started by drawing the rabbit at the top of a set of 10 stairs. We assigned a letter to each stair, and then each kid wrote a bunch of letter sequences representing the hops the rabbit makes. Kids came up with about 10 paths each before they started to want to find a faster way. My daughter suggested that you could first find all the paths that start with AB, and then all the paths that start AC.  I used this as a starting point. I asked the kids to consider just the last three steps in the staircase. If Leo is on step H, how many ways can he get to the bottom? Several kids were able to enumerate the 3 possibilities: HIJ, HI, or HJ.

Then I added step G. Now how many ways?  I pointed out that if the rabbit hops to step H, then his choices are now the same as the three ways we found for step H, namely: GHIJ, HI, GHJ. But Leo could skip step H, so we have to add in GIJ and GI as possibilities. Some kids understood this, but most did not. So I started even simpler.

What if there is only one step, step J? Then there is only one choice: J.

I ended up drawing a picture similiar to this:

At least one kid really seemed to understand that to get the ways for Step N, you add together the ways down from N-1 and N-2 (since Leo could hop down to either of those). All the kids soon saw that to fill in the next step, you should add the numbers from the two steps below, but many of them probably did not fully understand why. We were all impressed to get 89 ways, and were glad we didn’t try to enumerate them all.

Everyone started out quite engaged during this activity, but people started dropping off and getting distracted. In the end, 3 of the kids were still paying attention and 2 were quite ready for the activity to end.

YouCubed Heart

I intentionally made this activity much easier. YouCubed has a number of interesting questions about the picture, but I just asked how many rhombuses there were, and then let them color the picture for the last five minutes of circle.

Finishing the Fives (Age 8)

The Activities

1. Topic: Logic. Book: Sideways Arithmetic From Wayside School, by Sachar. Chapter 2.
2. Topic: Arithmetic, Patterns. Make the numbers 1 – 60 using only fives. For example, 26 = (5×5) + (5/5).

How did it go?

We had three kids for circle. Everyone was very focused, and followed my rule that we cannot draw Pokemon during Math Circle.

Sideways Math

The kids love the story of this book, and the problems were great for sideways thinking. First we reviewed the chapter from last week, since David led that circle. The kids were able to quickly explain why elf + elf = fool.  The rules are that each letter stands for one number 0..9, and each letter is a different number. The key to this one is that fool has an extra digit than elf, so we know e + e results in a carry. This means f must be a 1, which can be used to solve all the other letters too.

After this review, we read chapter two. In this chapter, Sue gets very upset because she thinks it’s weird to add words. Instead you should add numbers! Like 1 + 1 = 2!

The teacher writes that problem on the board as:

one + one = two

Sue says no! You should put the numbers there, not words! The teacher says, what numbers? Sue says “1 and 2!”. The teacher laughs: but there are no 1s or 2s in the answer!

Then we worked together to solve this problem, knowing that none of the letters stands for a 1 or 2.

We figured out that o must be < 5 because it shouldn’t cause a carry. o can’t be 1 or 2. It can’t be 0 because that would force ‘e’ to also be 0.  o can’t be 3 because there’s no number such that e + e = 3. So o must be 4.

At that point we got stumped because e + e = 4, but e is not allowed to be 2. We couldn’t figure out our mistake, so I checked the solution at the back, and realized, of course, that e + e must be 14. Then we quickly solved the rest of the problem.

Sue, in the book, then starts shouting out a bunch of math facts like: one + two = three, four + seven = eleven, and all the kids laugh at her. The teacher laughs to and says it’s impossible. So our next task was to prove that those problems are impossible.

one + two = three.  We quickly realized that there are no three digit numbers that add to a five digit number.

four + seven = eleven. This one was much trickier. Our intuition was that too many numbers have to be zero for this to work, e.g. u + e = e, o + v = v, f + e = e. But we had trouble proving it was impossible because what if there were carries involved? In fact, I thought I had proved it, until a kid explained that maybe u + e = e because r + n caused a carry. So really 1 + u + e = e + 10, which is possible if u is 9 and e is 7, for example. So we didn’t quite get a satisfying proof.

five + two = seven. I did most of this one myself. First I figured out that i + t must carry to the f, so that f + 1 = se. That means f = 9, s = 1, e = 0.  But we also know e + o = n, but that’s impossible if e is zero, because e + o must then equal o.

At this point the kids started to get a bit antsy. Some kids wanted to read the next chapter because the story is so funny, but no one really wanted to work on any more problems, so I ended the activity here.

Fives Chart

Two weeks ago, the kids filled out about half of chart where you compute the number 1 – 60 using only fives. For example, twenty is (5 x 5) – 5. We promised them a small prize if they could get 40 of the numbers completed, and another prize if they could fill them all in. This week, one of the kids realized that if the chart contains the answer for a number like 40, you can easily compute 39 and 41 by adding or subtracting 5/5.  This allowed them to quickly finish the whole chart. They still were pretty interested in using smaller numbers of 5s when possible, recognizing that it is not very elegant to write 5/5 fifty eight times to get 58.

Here’s a part of their chart:

 

 

 

 

Taking a Finger Walk (Age 6)

The Activities

1. Topic: Puzzles: Book: Taro Gomi’s Playful Puzzles for Little Hands.  We’re most of the way through now, probably one circle left of puzzles.
2. Topic: Logic: I printed sheets with 6 uncolored flowers on one side, and 9 on the other.  There were two puzzles: For 6 flowers, “There are more red flowers than purple, and more yellow flowers than red.  For 9 flowers, “There are more red flowers than purple, more blue than red, and the same number of blue and yellow.”
3. Topic: Spatial Reasoning:  Corey and I built a number of models out of Legos.  The kids each picked a model and had to copy it exactly.  They could pick it up and look at it from any angle.  Each kid copied several models.
4. Topic: Attributes, Games:  We played a couple rounds of Set with just the solid cards.

How Did It Go?

We had four kids this week.  One kid had been gone for a couple months, but now everyone is back from summer trips.  This circle went well, the kids were all interested in all the activities.

Playful Puzzles

We spent quite a bit of time on a puzzle with two kids at either end of a very windy path, with the question “Where will they meet?”  We measured by placing coins from either end.  They also enjoyed a page where you were supposed to “take a walk” with your finger by tracing a path and following various instructions along the way (e.g., “Take a rest here” or “Go around this corner really fast”).  Every kid did it once.

Flower Logic

The kids figured out the answers pretty quickly.  Interestingly, different kids figured out the second one from the first.

Lego Models

Different kids definitely had different skill levels on this one.  One kid breezed through a whole bunch, while others took quite a bit longer.  The trickiest ones were the dinosaur, because it was irregular and a bit complicated internally, and an offset colored square because it was tricky to get the right pattern of blocks on the bottom row (the kid working on it initially had the colors going the inverse rotation).

Set

We’ve played before with this circle, which the kids remembered, but not all kids remembered the rules.  Our son has played a lot, so after he got a few I said he had to let other kids get sets.  I was happy because all the other kids got at least one set on their own.

Elf + Elf = Fool (Age 8)

The Activities

1. Topics: Codes, Arithmetic, Logic:  We did the first activity from Sideways Arithmetic from Wayside School by L. Sachar.  In this activity, you have to solve letter-number substitution problems like “elf + elf = fool”, “egg + egg = page”, “top + tot = opt” and “ears + ears = swear”.
2. Topic: Arithmetic:  We revisited the activity where you have to make as many different numbers from 1-60 using only 5’s and the four basic arithmetic operations (plus parentheses).  This time I gave them a prize based on how many they could come up with working together.
   

   

How Did It Go?

I started circle with a talk about the goals of math circle, with three points: 1) The activities are supposed to be hard and strengthen your brain (mentioning that just like soccer, you practice to get better and stronger), 2) The activities often will be things you haven’t done in school, and 3) Even if you think an activity is boring, if you say that it might affect the other kids, plus if you try hard you might find it’s actually interesting.

Whether due to this talk or not, circle went much better this time.  The activities were fairly tricky and all five kids contributed to both activities and paid attention most of the time.

Elf + Elf = Fool

The first one I had to give them some fairly strong clues before they realized that ‘f’ had to be 1.  After that they mostly figured out the rest.  “egg + egg = page” is quite a bit harder, the kids came up with all the key ideas but I steered them some.  “top + tot = opt” went even better, and by the 4th or 5th one some of the kids were getting pretty comfortable.

Formula 5

We’ve done this a couple times before with less progress than I had hoped, but this time went much better.  Besides the pep talk, I did two things differently: I had a chart on the wall where they could add their answers, and I gave them 1 prize at 25 answers, 2 at 40, and 3 if they got all 60.  In about 25 minutes they got 32 unique answers.  They also figured out the idea of adding or subtracting (5 / 5) repeatedly, but they didn’t use it to grind out all 60 numbers.  Initially they had (5 / 5) + (5 / 5) + (5 / 5) for 3, I challenged them to find a better way and they eventually got (5 + 5 + 5) / 5.  We’ll probably give them a chance to get the rest next time.  Also, a good variant we should do in the future is giving them a challenge like “Make 5, 13, 19, 27, and 41 using as few total 5’s as possible” with prizes based on how few — there’s lots of really interesting math in figuring out the factors and figuring out what nearby numbers can be made cheaply (similar to dynamic programming if you’re familiar with that concept from computer science).

A Pride of Fish? (Age 6)

The Activities

1. Topic: Comparisons: Book: Too Tall Tina by D. Merritt.
2. Topic: Measurement: I gave each kid a 12″ ruler and asked them to look around the first floor for something 3″ long.  Then I asked 6″, 11″, and 1″.
3. Topic: Verbal Discussions: I asked the kids a bunch of questions about what you call groups of things: cows (herd); sheep, birds (flock); wolves (pack); flowers (bouquet, bunch, garden); fish (school); geese (gaggle); cats (?); ants (colony); bees (hive, swarm); lions (pride); people (crowd); whales (pod); witches (coven); rabbits (warren); thieves, robbers, musicians (band); soccer players (team); dancers (troupe, company); soldiers (troop, army, legion); girl/boy scouts (troop); kittens, puppies (litter); math students (circle); cards (deck, pack); grapes, bananas (bunch); books (shelf, stack, library); wheat (field); hay (bale); knives (rack); ships (fleet); stars (galaxy, cluster, universe); planets (solar system); sailors (crew); actors (cast).
4. Topics: Logic, Numbers: I did an activity from  Math Logic & Word Problems, Gr. 1-2, Guess Benny’s Number and Guess Jenny’s Number.  Each had a series of clues that narrowed down to a single number.  We used a 100 Number Board to keep track of which numbers were eliminated.The first puzzle was
   1. The number has two digits.
   2. Both digits are greater than or equal to 5.
   3. The tens digit is greater than the ones digit.
   4. The sum of the digits is 12.
      

   The second puzzle was

   1. The number has two digits.
   2. Both digits are less than 8.
   3. The ones digit is greater than the tens digit.
   4. The sum of the digits is 10.
   5. The number is even.
5. Topics: Counting, Games:  Using the 100 board again, we played the following game.  Each turn, a kid rolled a six-sided die.  They could then advance that number of spaces up to 10 times (so if they rolled a 5, they could advance 0, 5, 10, …, 45, 50).  The goal was to get to 100.  The first time they started at 0, but the second time I had them start at 1 since it’s more interesting.

How Did It Go?

We had three kids this week.

Too Tall Tina

Not much math in this book, but loosely ties into the next activity.

Finding Objects

Some of the kids needed some help measuring at first.  One of the kids spent a lot of time measuring different parts of their mom’s body.  They were pretty excited when they found matching things.

Groups

The kids weren’t able to think of many of them — e.g., for cows, they only knew herd once I told them.  One of the few that they did get was bees, where our son got both “hive” and “swarm” right away — which is pretty funny, because he’s rather afraid of bees.  They also got band of musicians, circle of math students, pack and deck of cards, and solar system of planets.  One kid guessed “pride” for fish, and then when we got to lions realized that it actually went with lions.  For stars, with some help one of the kids thought of pictures in the sky, but couldn’t remember the word constellation.

Guess Jenny’s Number

This activity was kind of hard for them.  First, they weren’t that familiar with the concept of ones and tens digit.  Second, it’s pretty tricky that you need to cover all the squares that DON’T match.  They kept trying, though, and with some help, they were able to do it.  One neat thing is you get some nice patterns along the way.  Our 8-year-old daughter worked on one of them after circle, and it wasn’t trivial for her either.

Skip Counting

This was a good exercise for skip counting — the game made it a bit more interesting, but mostly it was about practicing skip counting.  Switching to starting at 1 made for a much more interesting game — the first time, two players finished in 3 rolls.  One of the kids realized that once you were on 96, if you rolled a 3, you should stay on 96 because there are more ways to win, which is the most interesting part of this activity.